
●日本の夏は暑かった
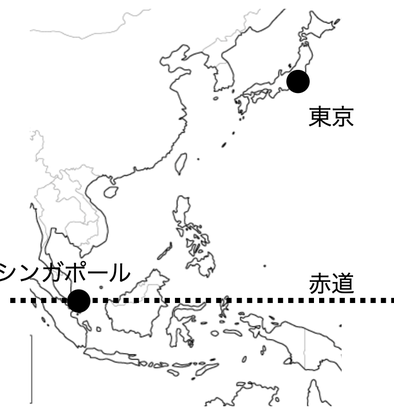
私は、2010年の夏、赤道直下のシンバポールと、少し北のインドに行ってきました。日本に帰ってきて、いろんな人から「暑かったでしょう」と言われました。実は「日本の方が暑かった」のです。それが実感でした。
そんなとき入江さんの文章に出会いました。おもしろかったです。ただ「日本はなぜ暑いのか」については、はっきり答えが出ていない気がしました。入江さんは言います。
地球の公転によって、地表を照らす太陽光の角度は少しずつ変化します。そのため、地球上の多くの地域に夏と冬が生じます。(入江洋一「世界各地の寒暖差」『たのしい授業』2010.11月号)
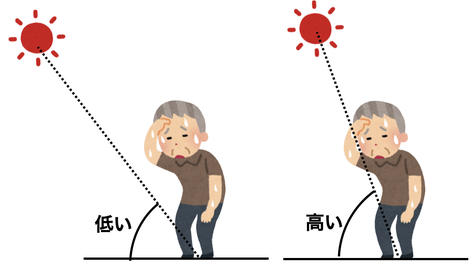
本当にそうでしょうか。夏の暑さは「太陽高度」とともに「昼の長さ」も気になります。そこで問題です。
[問題1]
夏至の日の昼の時間は、東京(北緯36°)とシンガポール(緯度0°)とを比べます。夏至の日に昼の時間は
ア. 東京の方が長い(1時間以上)
イ. シンガポールの方が長い(1時間以上)
ウ. 同じくらい(1時間以内)
[答え]
「国立天文台」に「暦計算室」というサイトがあります。それによると、6月20日の日中時間は
東京 14時間35分
シンガポール 12時間07分
東京の方がシンガポールより「2時間半(1.2倍)」長い(アが正解)。
[問題3]
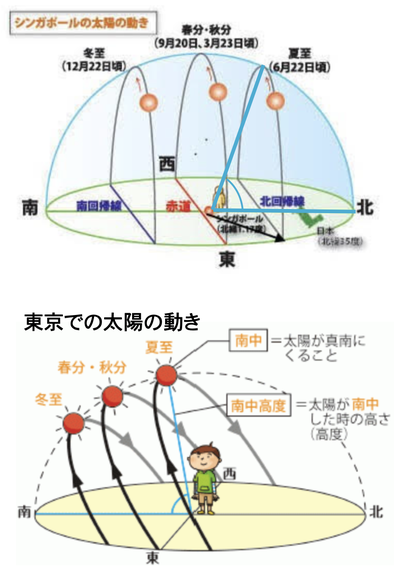
夏至の日の「太陽の南中高度」は、東京とシンガポールとでどちらが高いでしょう。
ア. 東京の方が5度以上高い。
イ. シンガポールの方が5度以上高い。
ウ. 同じ(違っても5度以内)
あさあ、「暦計算室」を見てみます。
夏至の日の太陽の南中高度は
東京 78度 シンガポール 67度
答えは「ア. 東京の方が1.16倍(76÷67)高い」
(まとめ)
東京の夏至は、赤道上と比べて日中時間が1.2倍長い。太陽高度は1.16倍高い。
ということは
「東京の太陽エネルギー=シンガポールの太陽エネルギー✖️1.4倍(1.2✖️1.16)」
つまり「夏至の太陽エネルギー(地表が受ける)は、
東京の方がシンガポールより1.4倍、大きい。
「太陽をストーブとすると、夏至の日は、ストーブのダイヤルが最高、最高出力」ということです。
でも、こんな単純な計算でいいのでしょうか。
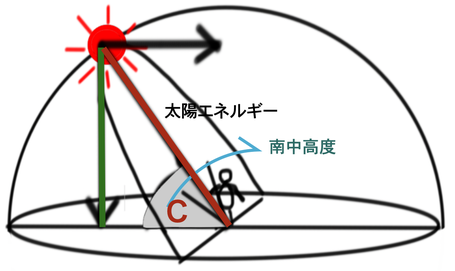
上の場所で、
真昼に地表が受ける「太陽エネルギー」は
太陽エネルギー= sin C ✖️ 太陽エネルギー
太陽の高さは,時刻によって変わりますが,まずはだいたいのことが知りたいので「南中高度」と使うことにします。
地表が「一日」に受ける
太陽エネルギー= sin C ✖️ 太陽エネルギー
sinを使って計算しなおすと
夏至の日の太陽の南中高度 東京 78度(sin78=0.98) シンガポール 67度(sin67=0.92)
0.98/0.92=1.07
6月20日の日中時間 東京 14.5時間 シンガポール 12時間(いつでも12時間)
14.5/12=1.2
「東京の太陽エネルギー=シンガポールの太陽エネルギー✖️1.28倍(1.2✖️1.07)」
●地球全体で、夏至の日の太陽を見てみると
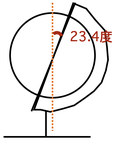
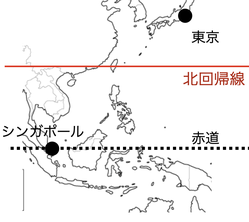
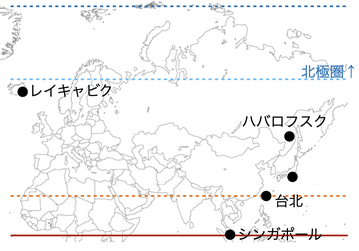
(1)「夏至の日の南中高度(世界)」
いちばん高いの「北回帰線」の上、台湾のほぼ中心を通ります。
北極点では、23.4度(地軸の傾きと同じ)になります。
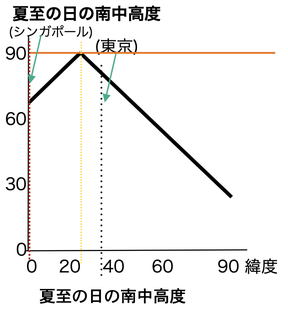
(2)「夏至の日の昼間時間(世界)」
右のグラフを見てください。北緯66.6度(90-23.4)以上(北極圏)になると「沈まぬ太陽」になります。
(3)「夏至の日の太陽エネルギー」
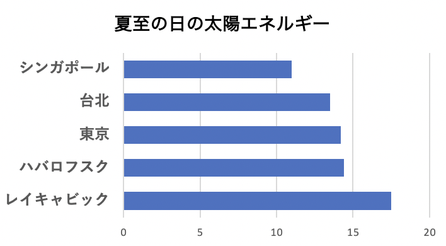
2つのグラフから「夏至の日の太陽エネルギー」を5都市で計算すると

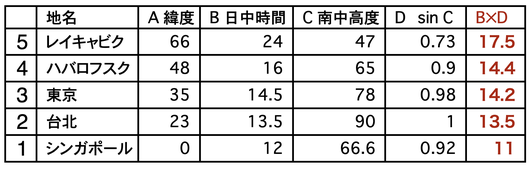
上の表をグラフにすると右のようになります。
なんと「レイキャビク」がいちばん大きくなりました。緯度が高いほど「太陽エネルギー」は大きいのです。
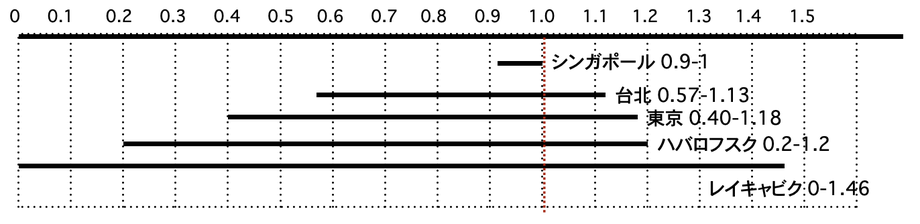
●地球全体で、太陽エネルギーの量を見る
下のグラフは、冬至から夏至まで、各地の太陽エネルギーの変化を表したものです。
「シンガポール (緯度0度)の秋分,秋分のエネルギー」を1にしてあります。
●実際の夏の暑さを調べてみる
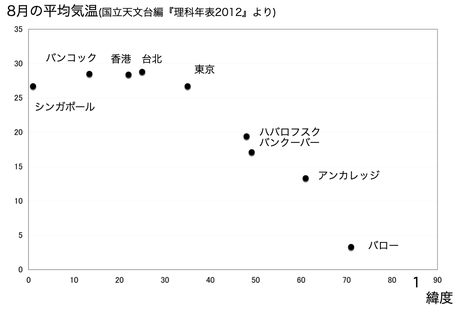
世界の8月の平均気温をグラフにしてみました。(『理科年表』より,北半球の主な海岸沿いにある都市)
やはり「東京」は、熱帯地方の都市なみに暑いようです。
●結論
季節による気温変化は、次の2つが関係する。
1 太陽の高さ
2 昼間時間の長さ
だが、緯度の違う各地を比べてみると
「昼間時間の長さ」の方が影響が大きい。
いかがでしょうか。
●補足1 正確に「積分」を使って計算する
「夏至の日に、一日の総日射量がもっとも多いのは「北極」です。それは積分を使って計算しないといけません。
●64
夏至の日に、一日の総日射量がもっとも多いのは、北緯何度の地点ですか。ただし次の仮定をおきます。
1 太陽は点とみなす。
2 地球は完全な球で、一定の角速度で自転する。
3 大気の吸収、屈折などの影響はまったくないものとする。
4 日射量は太陽の角度角がhのとき、sin h に比例するものとし、一日の総日射量 S は、それを日の出から日の入りまで合計(積分)したものとする。ただし北極圏以北の土地で、太陽が沈まないときは、24時間全体にわたる積分をとる。
5 夏至の日に、太陽の赤緯 β=23°27' で、tan β=0.4338とする。
(ヒント) 緯度φがの地点で時角(天球の北極から太陽と天頂を結ぶ二つの大円のなす角)tのときの太陽の高度角hは(球面三角法の公式、あるいは立体解析幾何の簡単な計算により)
sin h = sin β sin φ + cos β cos φ cos t
で与えられます。Sの形が φ+β ≦ π/2 のときと
φ+β ≧ π/2 のときとでちがうことに注意してください。
(答え)
(1)

(2)

(3)
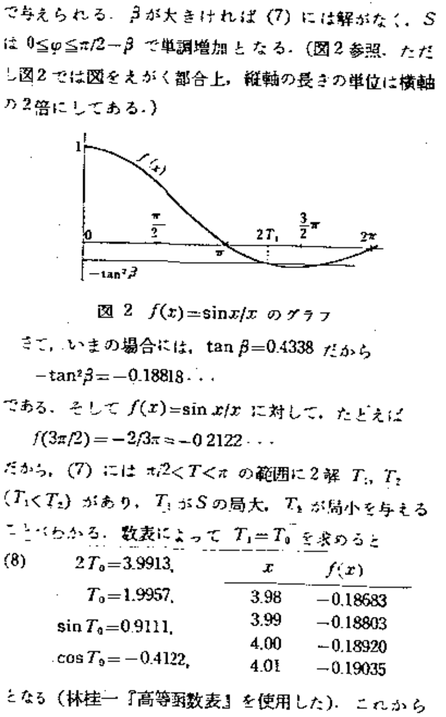
『大学への数学』(雑誌,東京出版)より
(4)

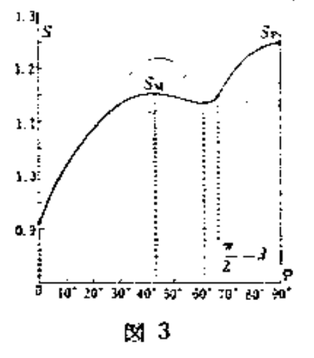
補足2 緯度別に「年間総放射量」を求める
右は「Gnuplot」というツールを使って、「年間総放射量」を描いたものです。それぞれのグラフを切って重さを測ってみました。
(緯度0°を「1」とすると)
緯度0° 5.4 g 1
緯度15° 5.1 g 0.94
緯度 30° 4.7 g 0.87
緯度 45° 3.8 g 0.70
緯度 60° 3.1 g 0.57
緯度 75° 2.3 g 0.42
緯度 90° 2.2 g 0.37

奈佐原顕郎(筑波大学農林工学系)「応用、太陽高度の計算」より(2010検索、2022.10.30検索できず、削除?)
日本で受ける太陽の総放射量は「北緯36°」くらいなので、「赤道の0.8倍」くらいになります。
